一、排序
1.桶排序
int main()
{
int a[11],i,j,t;
//初始化数组
for(i=0;i<=10;i++)
{
a[i]=0;
}
//读入五个数用于排序
for(i=1;i<=5;i++)
{
scanf("%d",&t);
a[t]++;//a[t]记录分数t的出现次数
}
for(i=0;i<=10;i++)//依次判断a[0]-a[10]
{
for(j=1;j<=a[i];j++)//分数i出现的次数a[i]
{
printf("%d",i);//打印分数i
}
}
return 0;
}
时间复杂度O(M+N)
2.冒泡排序
核心在于双层嵌套循环
分数排序:
int i,j,t,n;
int a[100];
printf("输入需要排序的个数:");
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
for(i=1; i<=n-1; i++)//n个数需要排n-1趟
{
for(j=1; j<=n-i; j++)//每一趟需要比较n-i次大小
{
if(a[j]<a[j+1])//交换位置,从小到大
{
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
}
}
for(i=1;i<=n;i++)//打印排好序的数字
{
printf("%d\n",a[i]);
}
return 0;
根据分数打印人名:
struct student{
char name[21];
char score;
};//创建一个结构体存放姓名和分数
int main(){
int i,j,n;
struct student a[100],t;//创建一个数组用来存放姓名和分数
printf("输入一个n:");
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%s %d",&a[i].name,&a[i].score);//分别存入姓名和分数
}
//排序
for(i=1;i<=n-1;i++)
{
for(j=1;j<=n-i;j++)
{
if(a[j].score<a[j+1].score)//数组中的分数进行比较
{
t=a[j];//交换保存着姓名和分数的数组
a[j]=a[j+1];
a[j+1]=t;
}
}
}
for(i=1;i<=n;i++)
{
printf("%s %d\n",a[i].name,a[i].score);//打印排好序的姓名和分数
}
return 0;
}
时间复杂度为O(n^2)
3.快速排序
二、栈 队列 链表
1.队列
允许在队列的首部进行删除操作(head++),在队列的尾部进行插入操作(tail++);haed用来记录队列的队首(即第一位),tail用来记录队列的队尾的下一个位置。规定:队首和队尾重合时,队列为空。
问题:现有一串数字,删除第一个数字,第二个数字移到队尾;删除第三个数字,将第四个数字移到队尾......
队列是广度优先搜索以及队列优先的Bellman-Ford最短路算法的核心数据结构。
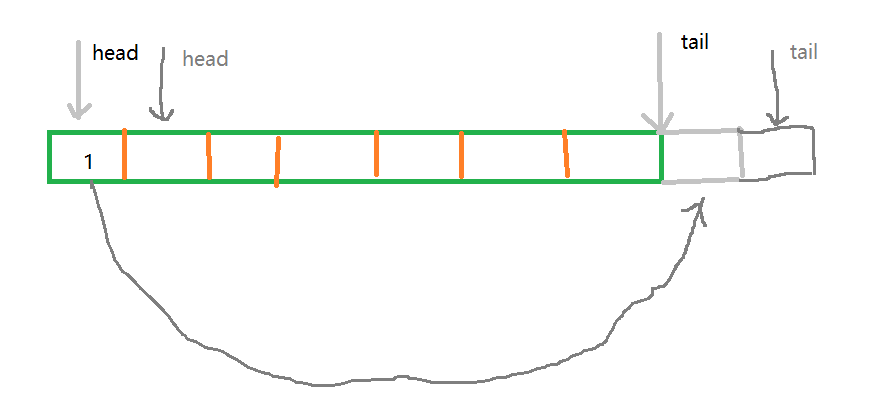
一般代码实现:
int main()
{
int q[102]={0,6,3,1,7,5,8,9,2,4},head,tail;//初始化队列
int i;
head=1;
tail=10;
while(head<tail)
{ printf("%d",q[head]);//打印队首
head++;//加1,指向新的队首
q[tail]=q[head];//将新的队首移到队尾
tail++;
head++; //再将队首出队,进入下次循环
}
return 0;
}
结构体实现:
struct queue
{
int data[100];
int head;
int tail;
};
//结构体包含整型数组data、整形head和整形tail,访问其内容,可用`.成员`
int main()
{
struct queue q;
q.head=1;
q.tail=1;
int i;
for(i=1;i<=9;i++)
{
scanf("%d",&q.data[q.tail]);//初始化队列
q.tail++;
}
while(q.head<q.tail)
{
printf("%d",q.data[q.head]);
q.head++;
q.data[q.tail]=q.data[q.head];
q.tail++;
q.head++;
}
return 0;
}
2.栈
栈:后进后出,只能在一端进行插入和删除操作。
回文:正读反读均相同的字符序列,如aha,ahha