C语言重难点-数据在内存中的存储、内存函数、动态内存分配

一、数据存储

1. 数据类型

类型的意义：

使用这个类型开辟内存空间（大小决定了适用范围）
决定了如何看待内存空间的视角

1.1 内置类型

（1）整形家族

char
有符号数，范围是[-128，127]
short
int
long

（2）浮点型家族

float：4字节
double：8字节

（3）指针类型

（4）空类型

void表示空类型，通常用于函数的返回类型、函数的参数、指针类型

1.2 自定义类型（构造类型）

数组类型
结构体类型 struct
枚举类型 enum
联合类型 union

此处见二、自定义数据类型

2.整形在内存中的存储

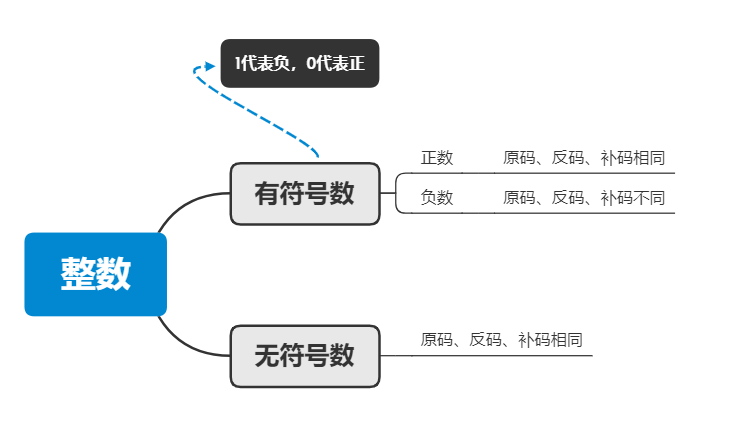
QQ截图20210828135840.png
（1）原码反码补码
计算机中的有符号数有三种表示方法，即原码、反码和补码。对于整形，数据存放内存中存放的是补码
8位二进制, 使用原码或反码表示的范围为[-127, +127], 即2^7-1，而有符号数使用补码表示的范围为[-128, 127]，-128就是10000000，无符号数范围是[0，255]；因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-2^31, 2^31-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值。
原码：
直接将二进制数按照正负数形式翻译成二进制就可以；
反码：
正数的反码是其本身
将原码的符号位不变，其它依次按位取反；
补码：
正数的反码是其本身
反码+1就是补码。
栗子：
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
正码、反码和补码详解
真值：现实世界中的数字
原码：在真值的基础上解决了正负号在机器中的表示问题
补码：在原码的基础上解决了如何将减法变成加法的问题
移码：在补码的基础上解决了数字的直观大小比较问题
（2）大小端
大端模式（大端字节序存储模式）：数据的低位保存在内存的高地址中，而数据的高位保存在内存的低地址中
小端模式（小端字节序存储模式）：数据的低位保存在内存的低地址中，而数据的高位保存在内存的高地址中

栗子：
判断当前机器的字节序：
//思路：将存储的地址存放在一个字符指针变量中，判断首元素和待比较的低位相等。
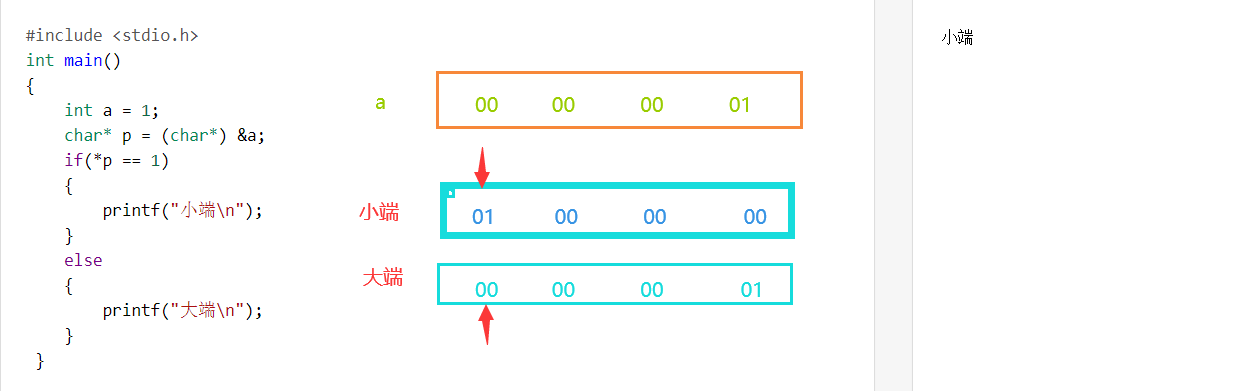
QQ截图20210828203335.png
将其封装成一个函数：
QQ截图20210828204128.png
指针部分可以简化成：return *(char* )&a;
（3）整型提升
表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。
表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

负数的整型提升
char c1 = -1; 变量c1的二进制位(补码)中只有8个比特位： 1111111 因为 char 为有符号的 char 所以整形提升的时候，高位补充符号位即1，提升之后的结果是： 11111111111111111111111111111111
正数的整型提升
char c2 = 1; 变量c2的二进制位(补码)中只有8个比特位： 00000001 因为 char 为有符号的 char 所以整形提升的时候，高位补充符号位即0，提升之后的结果是： 00000000000000000000000000000001
无符号整形提升，高位补0

（4）举个栗子
题一：
QQ截图20210828212735.png
（即使两个char类型8位的相加，在CPU执行时实际上也要先转换为CPU内整型32位操作数的标准长度。）
题二：

计算方法：因为整形存储的是补码，所以先计算出32位补码，后取8位char类型，遇到整型提升（%d），补充0/1至32位（此时还是补码），提升后输出将此时的补码转化成原码再转化成十进制即可。
原码——>补码（取后八位...）——>整型提升成补码——>原码输出

负数：补充1
正数：补充0
无符号unsigned：补充0

题三：

题四：

//这里的数是int类型，在计算时不需要取后8位整型提升；%d是输出有符号数，将相加后的补码，按照符号位不变的原则，算出对应原码即可。
题五：

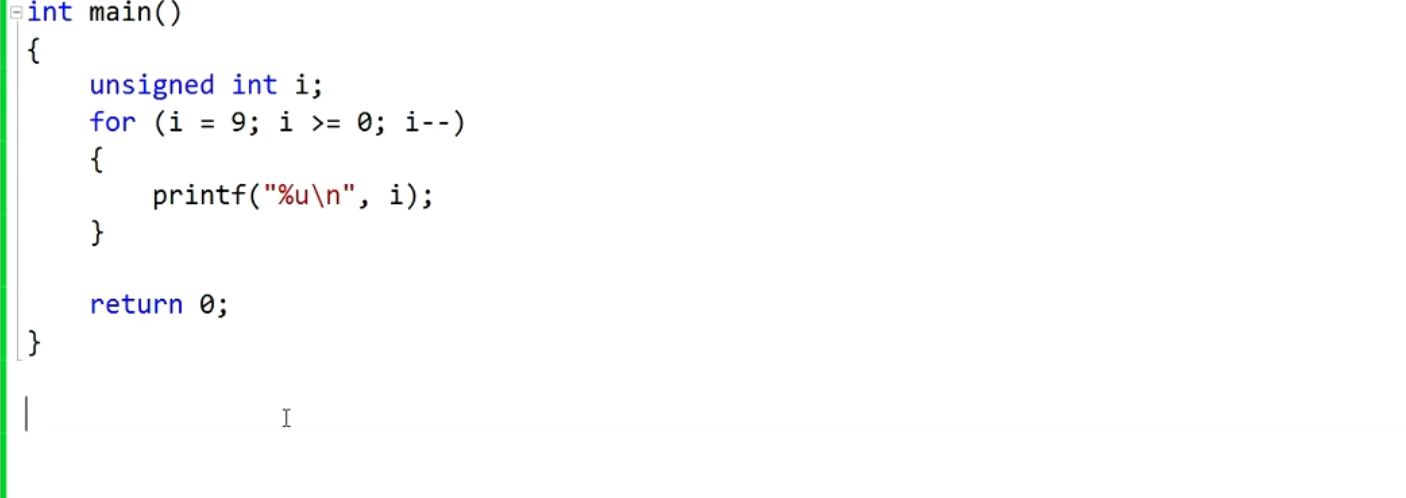
//因为i是无符号数始终>=0，此循环执行结果为：9，8，7，6，5，4，3，2，1，死循环。
无符号数取值范围：[0,255]；有符号数（char）取值范围：[-128,127]
题六：

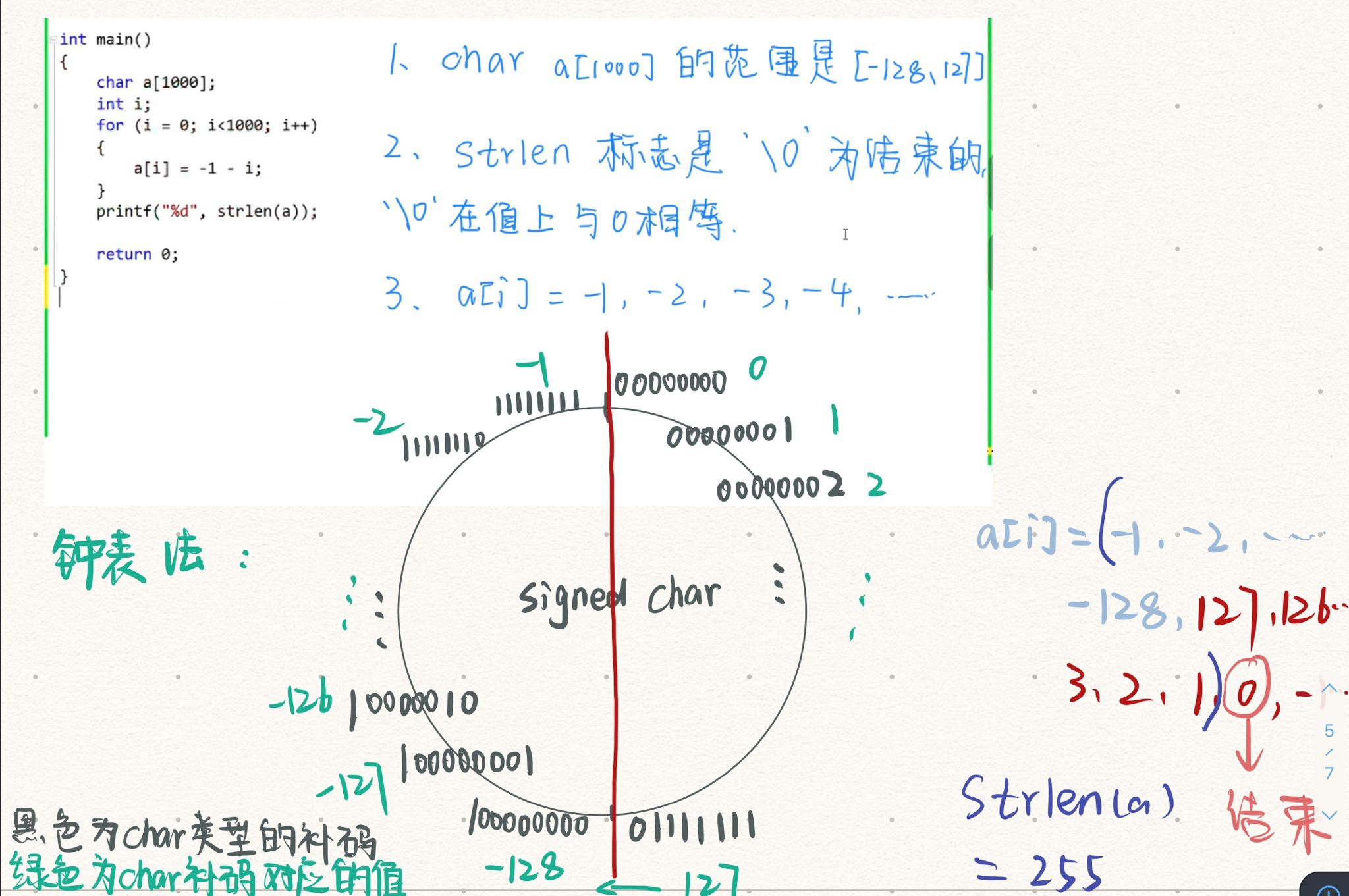
//此题注意有符号类型（char）的范围和钟表法

2.浮点型在内存中的存储

1.1 浮点数的表示方法

（1）表示方式：

S：符号位
M：1<=M<2，M可以写成1.~~~~~~形式，在计算机保存Mde时候，默认第一位总为1，故存储时只存小数点后的数，小数部分补齐0至32/64位，读取时再加上第一位的1。好处就是可以多存一位有效数字。
E：是无符号整数，若E为8位，它的范围是[0，255]；若E为11位，它的范围是[0,2047]。
因为科学计数法中E可能是负数，如十进制小数0.5它转换成二进制为0.1，写成科学计数法为（-1）^0`*`1.0`*`2(-1),所以IEEE 754规定，保存E时加上中间值，对于8位，加上127；对于11位，加上1023,这样保证了存入的E为正。
补充：关于二进制与十进制的转换

其中，E从内存中取出有以下三种情况：
①E不全为1或不全为0
举个栗子：0.5
（-1）^0`*`1.0`*`2(-1)：s=0,M=1.0,E=-1，E存入的位-1+127=126；对于32位来说，存储如下：

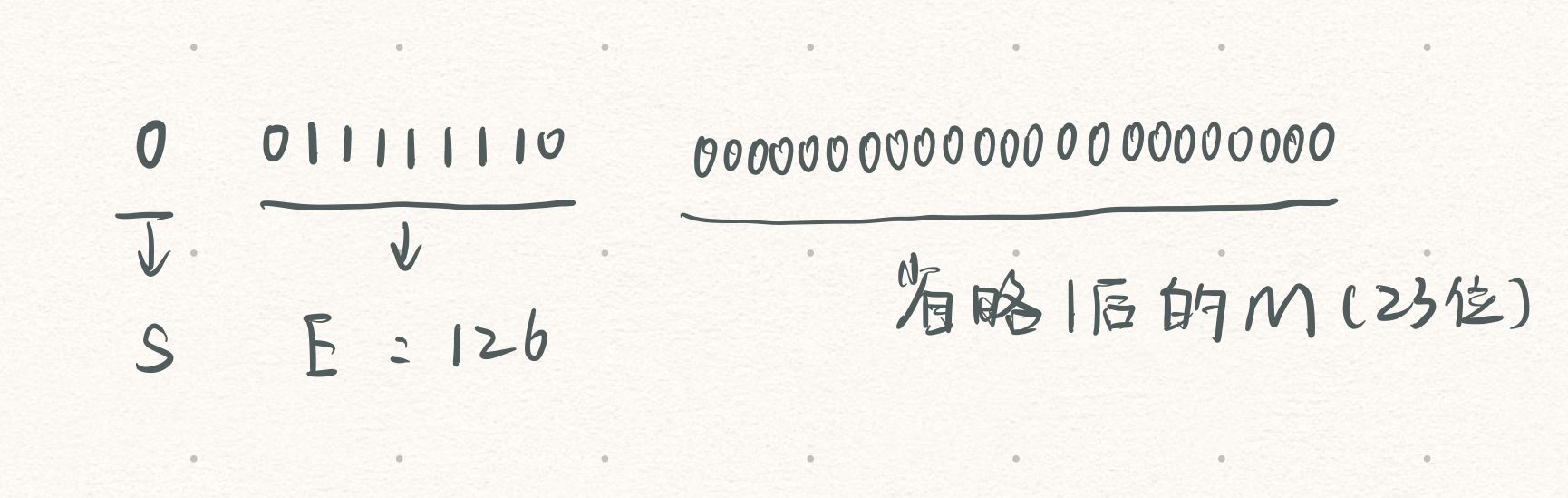
②E全为0
当E为0时，那么真实值为-127，那么V趋于0.
所以直接规定，当指数E存储值为0时，它的真实值为1-127，有效数字M不再加上1，直接写成+-0.几几几。
这样的好处就是可以表示+-0，以及接近于0的很小的数字。如：
0/1 00000000 01100000000000000000000——>+/- 0.011*2^(-126)
③E为全1
当E=11111111即255时，E的真实值为128，表示的数是正负无穷大的数字。

举个栗子：

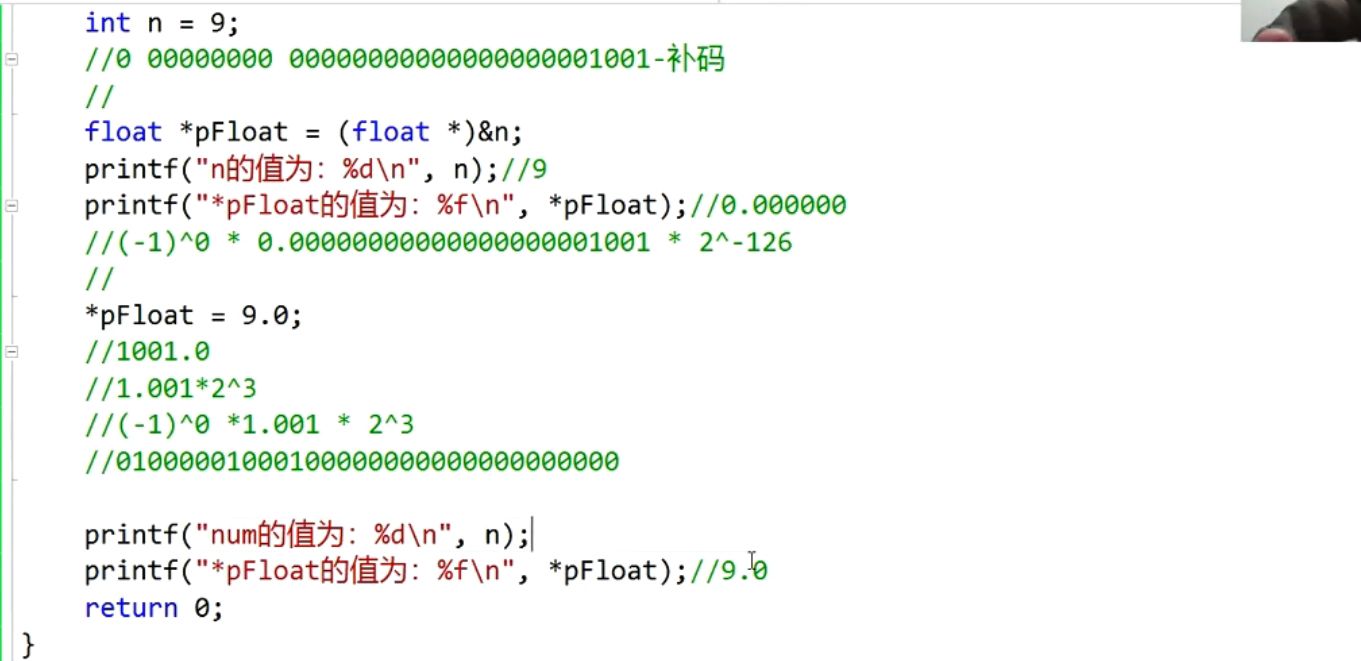
//n=9是整形，存入的形式是：符号位（1）+数值（31位）
即00000000 00000000 00000000 00001001
若要以%f输出，则将00000000 00000000 00000000 00001001看成是0 00000000 0000000 0000000000001001即S（1位）+E（8位）+M（23位）表示的数就是（-1）^0*0000000 0000000000001001*2^(-126) ，趋于0 。
9.0是float类型，二进制为1001.0，E存储值为127+3=130，存放形式是0 10000010 00000000000000000000000
若以整形形式输出，将其看成0（符号位） 1000001000000000000000000000000即可。

二、自定义数据类型

1.结构体

1.1 结构体类型的声明

结构是一些值的集合，这些值成为成员变量。结构体的每个成员可以是不同类型。
（1）结构的声明
声明格式：
struct tag
{
member-list;
}variable-liast;
//tag 是结构体标签。
member-list 是标准的变量定义，比如 int i; 或者 float f，或者其他有效的变量定义。
variable-list 结构变量，定义在结构的末尾，最后一个分号之前，您可以指定一个或多个结构变量。
在声明结构体时，tag、member-list、variable-list 这 3 部分至少要出现 2个：
①声明了结构变量，未声明结构体标签——又叫匿名结构体类型，必须要声明结构变量。
struct
{
int a;
char b;
double c;
} s1;
②未声明结构变量，声明了结构体标签
struct Su
{
int a;
char b;
double c;
} ;
③声明了结构变量，也声明了结构体标签
struct Su
{
int a;
char b;
double c;
} s1;

1.2 结构体的自引用

struct Node
{
int data;
struct Node* next;
};
可以使用 typedef 来为用户自定义的数据类型取一个新的名字。
typedef struct Node// 重命名时不建议省略结构体标签，若省略，则Node无声明。
{
int data;
struct Node next;
} Node;

1.3 结构体变量的定义和初始化

（1）定义
struct Su
{
int a;
char b;
double c;
} s1;//定义方式1：声明类型变量的同时定义变量s1

struct Su s2；//定义方式2：定义结构体变量s2
(2)初始化

s.c='c',s.a=100赋值也可以。
在结构体里包含结构体：

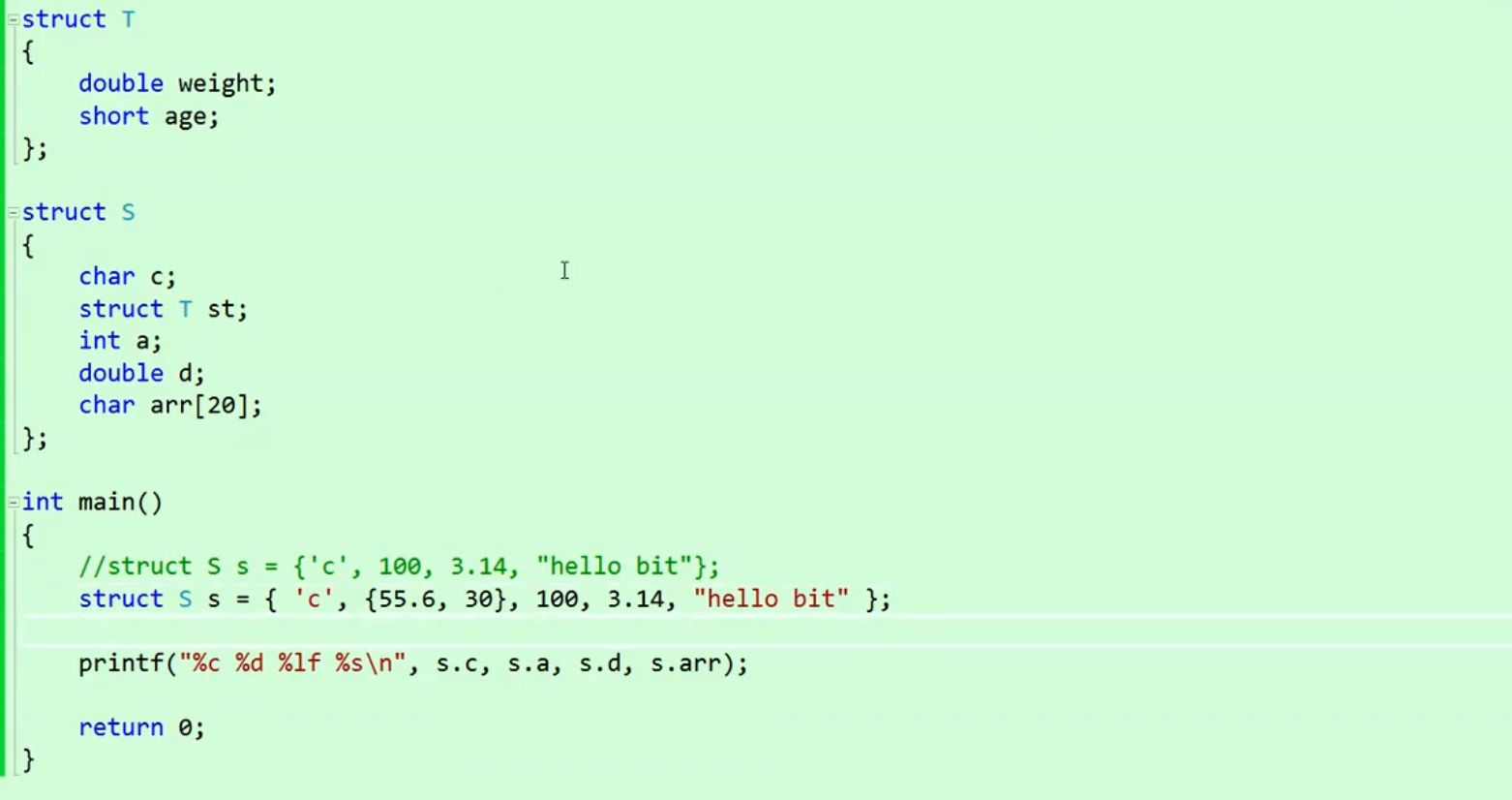
访问weight，用s.st.weight即可。

1.4 结构体内存对齐

（1）对齐原因

平台原因（移植原因）
并非所有平台能任意访问任意地址的任意数据，某些硬件只能在某些地址处取某些特定类型的数据。
性能原因
数据结构（尤其是栈）应该尽可能在自然边界对齐，因为若是未对齐的地址，处理器需要两次内存访问，而对齐的地址只需要访问一次。

（2）对齐规则

第一个成员在与结构体变量偏移量为0的地址处。
其他成员变量要对齐到对齐数的整数倍的地址处。这里的地址是相对于初始地址0而言，也就是偏移量。
对齐数=编译器默认的一个对齐数与该成员大小（最基本的数据类型的大小）的较小值。
char arr[5]//对齐数为1
结构体总大小为最大对齐数（每个成员变量都有一个对齐数）的整数倍。（不够就补齐空间）
如果嵌套了结构体，嵌套的结构体对齐自己的最大对齐数的整数倍的地址处，结构体的整体大小就是所有最大对齐数（含嵌套结构体的对齐数）的整数倍。

对规则的解释：
题1：

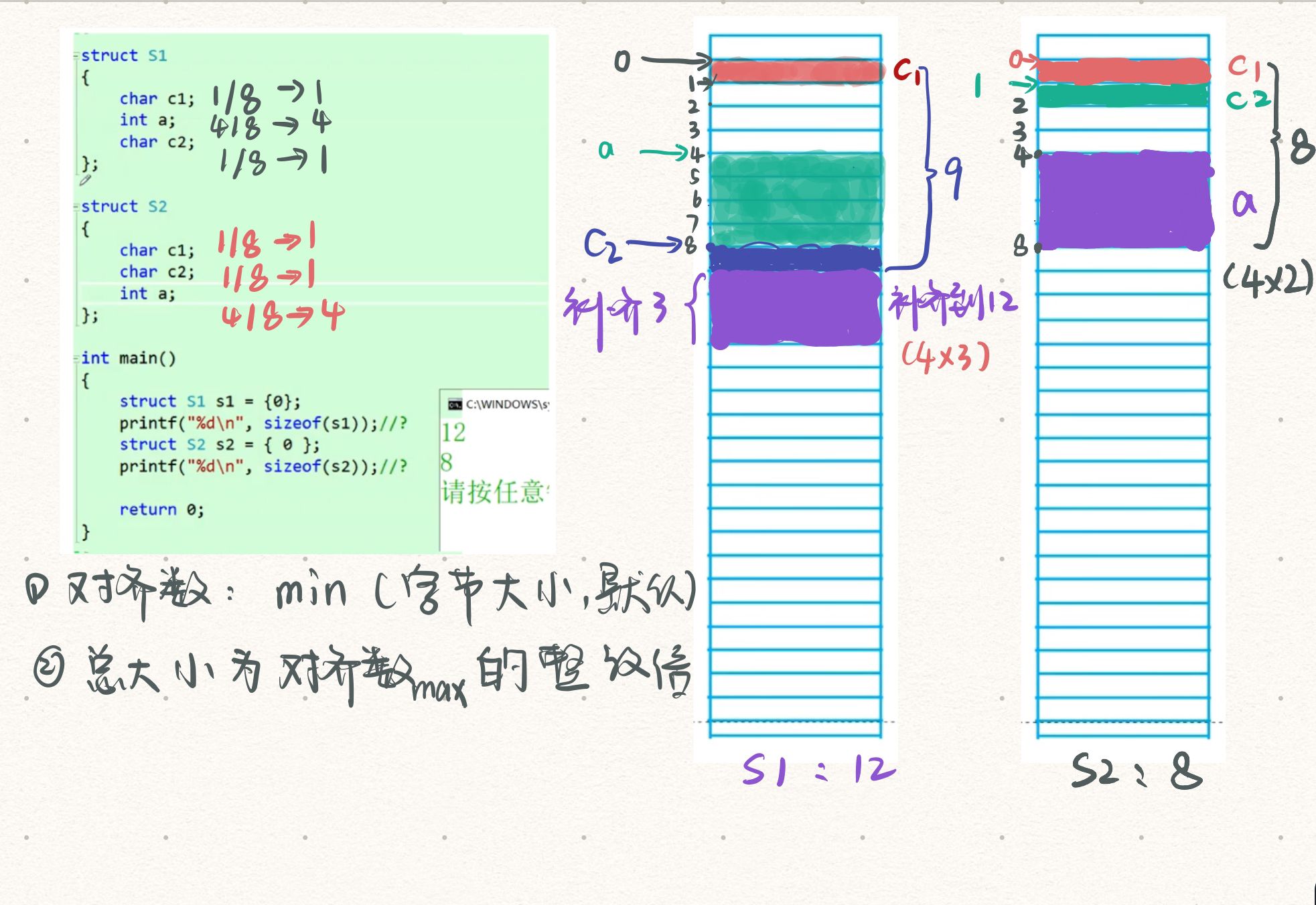
注：其中vs默认对齐数是8，gcc编辑器没有默认的对齐数，对齐数就是成员大小。
题2：

//由上可知，尽量让占用小的成员集中在一起。
题3：（结构体嵌套）

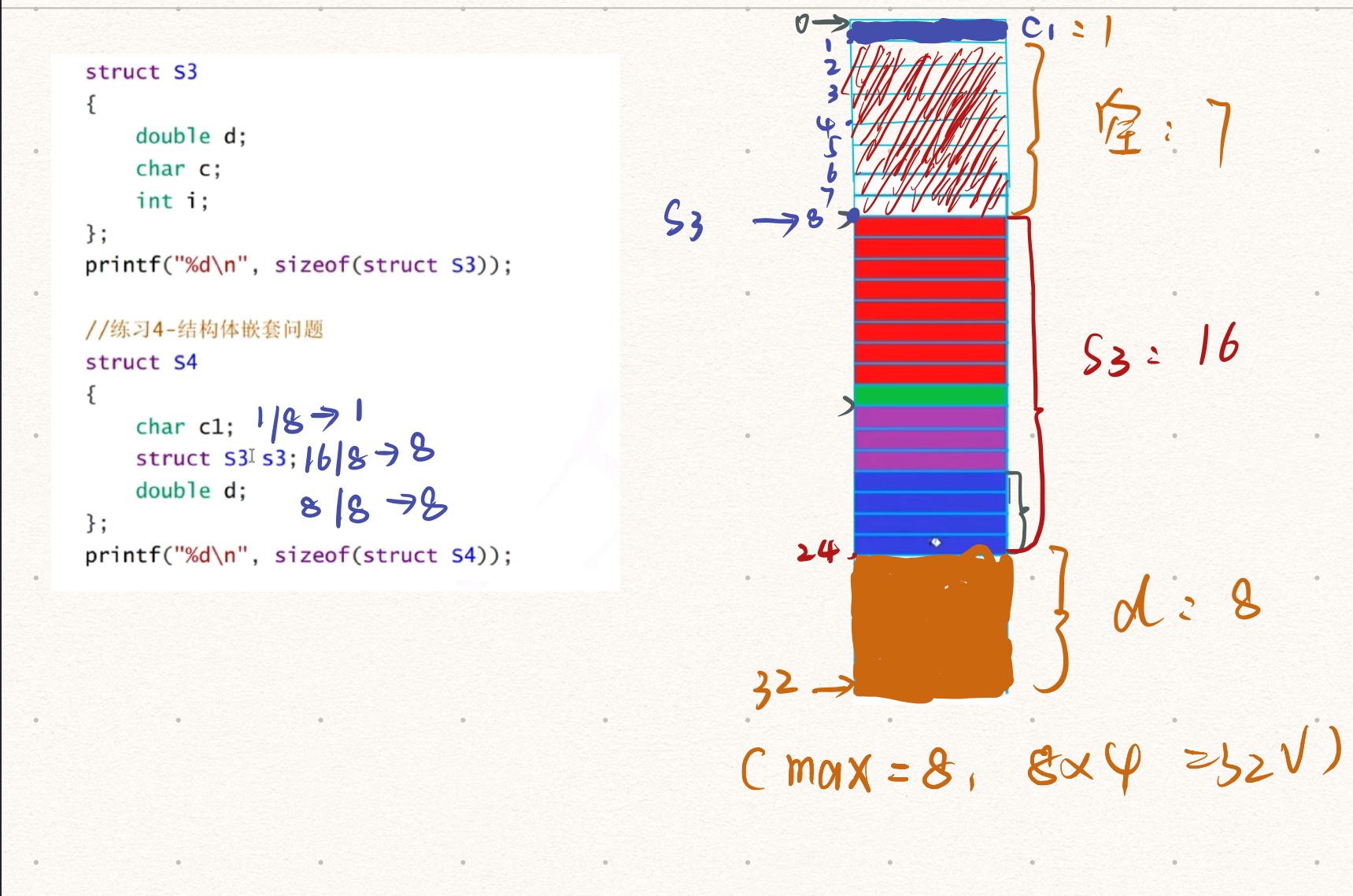
计算步骤：

（3）修改默认对齐数
#pragma pack(6)//设置默认对齐数为4，一般设置成2，4，8，16这样的数
#pragma pack（ )//取消设置的默认对齐数
补充：

引入头文件：#include <stddef.h>

offsetof()函数用来计算偏移量。

具体的之后更新。
........

1.5 结构体传参

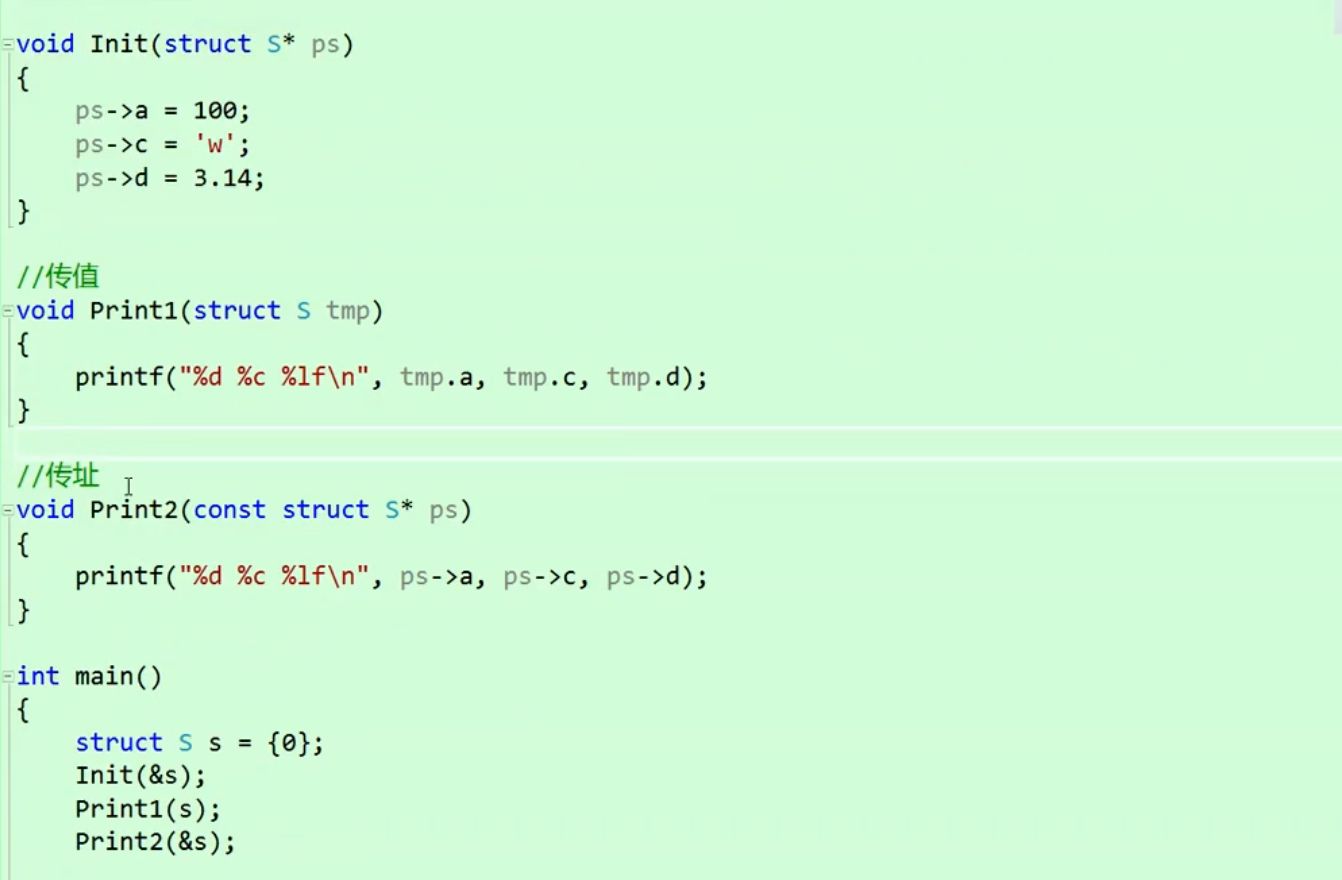
结构体传参的时候，要传结构体的地址

1.6 位段

(1) 位段的声明：

位段的成员必须是int，unsigned int，signed int。
位段的成员名后有一个冒号和一个数字，数字代表着二进制位。

struct S
{
int a : 2;
int b : 5;
int c : 10;
int d : 30;
};
//struct S s;
//sizeof(s)=8字节
(2)内存分配规则

位段成员可以是 int，unsigned int，signed int或是 char（整形家族）；
位段的空间上是按照需要以4个字节（int）或者是1个字节（char）的方式来开辟的；
位段：不跨平台，注重可移植的程序应该避免使用位段。

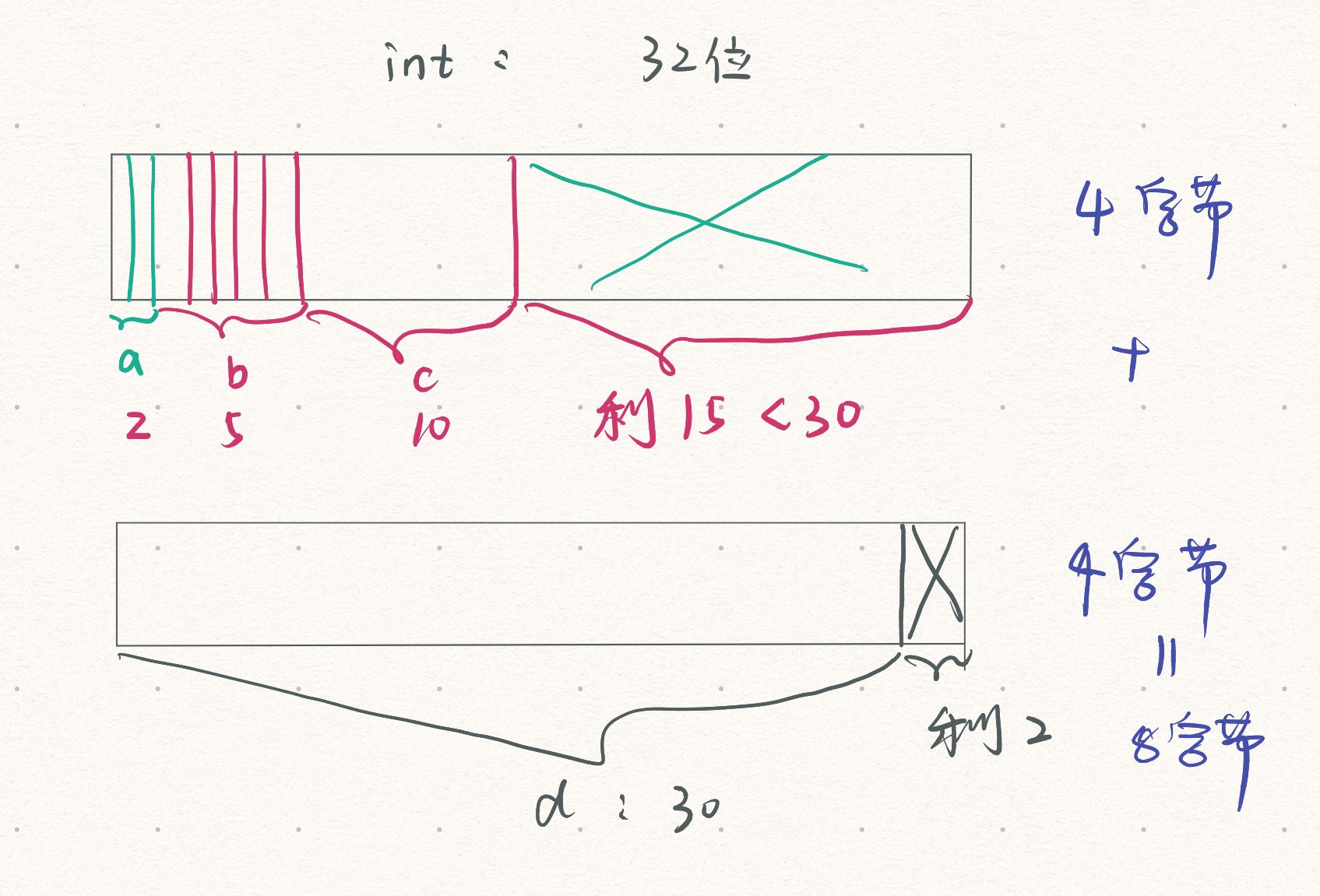
（3）应用
数据传输时的数据包

2.枚举

1.2 枚举类型的定义

enum Sex
{
//枚举的可能取值-常量
male，//male默认的值为0
female，//默认值为1
secret//默认为2，依次加1
};
除了默认值赋值外，也可以自己赋给常量一个初始值。

1.3 枚举的优点

（1）增加代码的可读性和可维护性
（2）与#define比较，枚举有类型检查，更严谨
（3）防止了命名污染（封装）
（4）便于调试，一次可以定义多个常量

3.联合(共用体)

1.1 定义

联合是一种特殊的自定义类型，定义的变量包含了一系列成员，特征是这些成员共用同一块空间。
union Un
{
char c;
int i;
};
union Un u;
sizeof(u)//4，大小至少是最大成员的大小;（满足4是最大对齐数4的整数倍）
//&u,&u.c,&u.i三者的地址一样，共用同一块空间
补充：用联合体判断大小端：

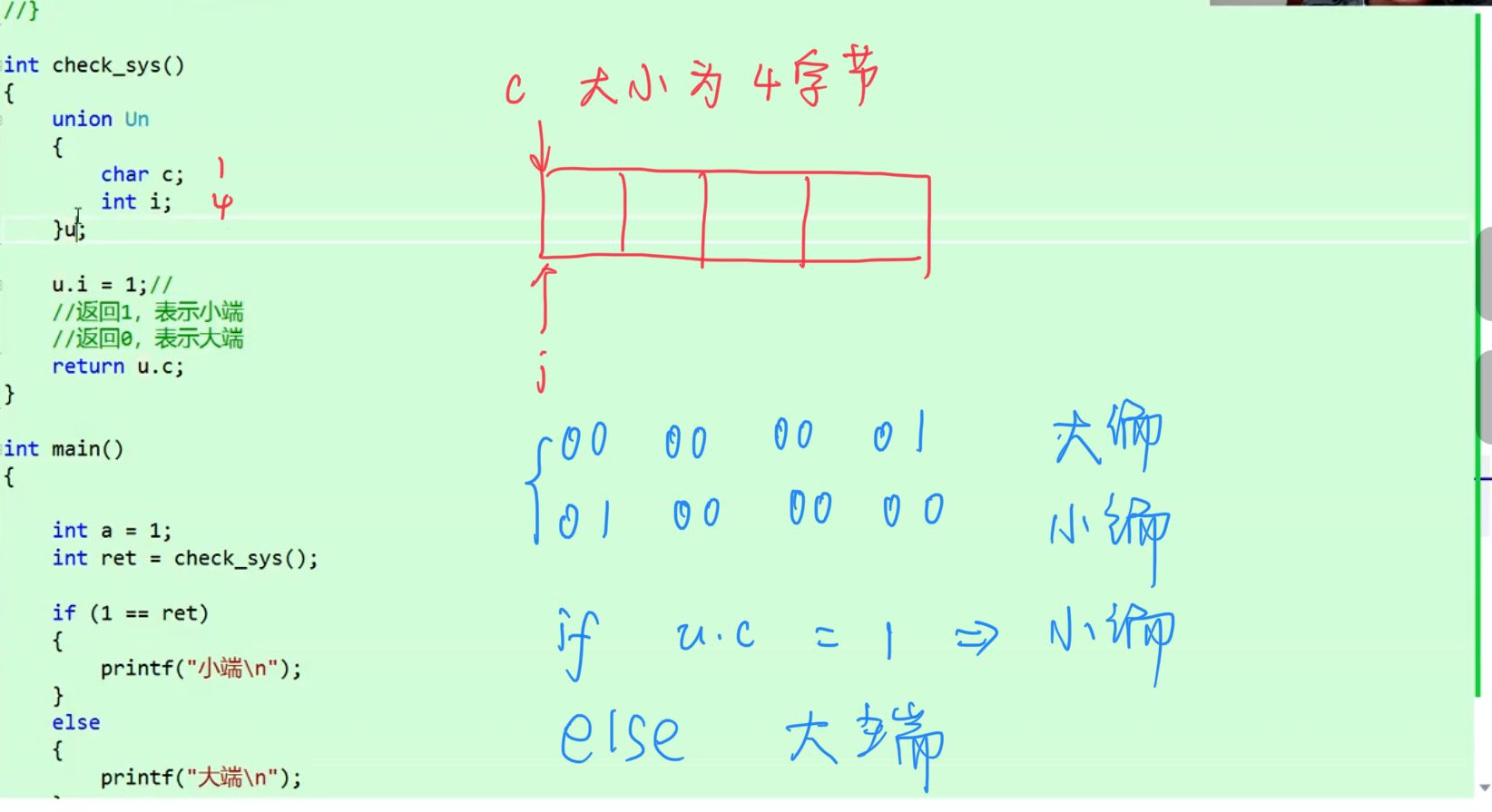
1.2 联合大小的计算

联合的大小至少是最大成员的大小
当最大成员的大小不是最大对齐数的整数倍的时候，就要对齐到最大对齐数的整数倍。

三、动态内存分配

1. 基本介绍

（1）内存的使用方式

创建一个变量
栈区：存放局部变量、函数的形式参数
堆区：动态内存分配
静态区：存放全局变量、静态变量
创建一个数组

在高处，凝望世界流动